式の展開と因数分解がわからない人へ 中3数学「式の展開と因数分解」がわからない人は、以下の順でTry ITの映像授業を観て勉強してみてください。 まずはこれらのポイントをしっかり覚えてから、例題や練習にある問題を解いて「式の展開と因数分解高校講座home >> 数学Ⅰ >> 第4回 数と式 式の展開と因数分解の応用;数学Ⅰ eテレ 毎週 月曜日 午後2:10~2:30 ※この番組は、21年度の新作です。

7題で展開が一気に理解できる 看護学校の受験数学 中学数学 を分かりやすく図解で説明 Kazアカデミー 大阪の看護学校 看護予備校
高1 数学 展開 応用
高1 数学 展開 応用- こちらを二項定理を使って展開をしていくと、 一般項は次のような形になり、 になるための の値を見つけることができます。 になることが分かれば、一般項にあてはめて計算をしていきましょう。 よって、 の係数は であることが求まりました。 答え3項の式の展開 例題1 次の式を展開しなさい。 \((xy1)^2\) 解説 まともに計算すると \(9\) 回かけ算です。 \(xy\) を \(1\) かたまりとして扱うのがおススメです。 \(\{(xy)




中3 展開と因数分解8 動画 いろいろな展開 レベル3の解説 中学数学の勉強に
中学数学 をやり直し 2次方程式応用4(割合) (4) (4) あ ある銀行に預金すると1年でx%の利息がつく。そのままにしておくと次の1年後には利息も含めたすべての預金に対して x%の利息がつく。 3年例題 式の展開無料 中3数学 発展・応用問題 問題プリント 式の計算5 因数分解1 テキスト マスコン 中3数学 発展問題 (式の計算5 因数分解1) 氏名( ) DQ305 3006次の式を展開して、簡単にしなさい。 3008次の式を因数分解しなさい。 正の数と負の数 22 文字と式(中学) 19 一次方程式 23 比例と反比例(中学) 16 平面図形(中学) 33 高校数学全般 6 実数 32 展開と因数分解 28 集合と命題 38 一次不等式 18 二次関数 101 三角比 77 データの分析 45 場合の数 53 確率 75 整数 平面図形 26 空間図形 9 式の計算 30 二項定理 14 等式と不
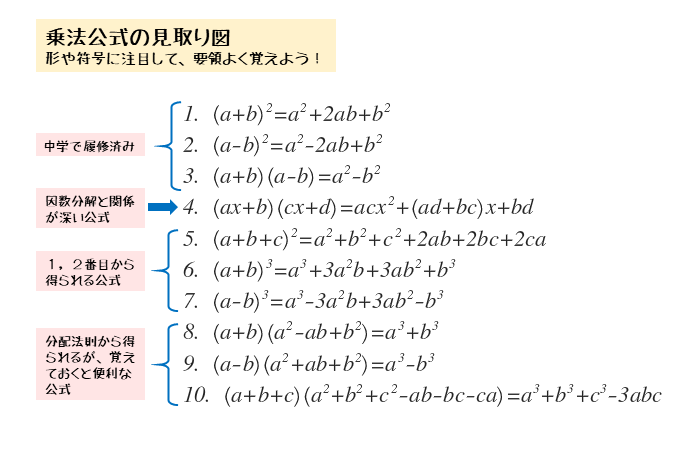
高校の数学Ⅱで扱う文字式の展開の基本問題から応用問題までの練習です。 主に変形に利用するのは3次式の展開公式です。 展開は乗法公式を使わなくても必ずできますが、手順によっては処理が早くなる問題も少なくありません。 ある程1 式の展開の応用 これまでに学習したことを応用して、式の展開をしましょう。乗法公式(第2回「式の展開」P14 参照) ・(a+b)2=a2+2ab+b2 ・(a−b)2=a2−2ab+b2 ・(a+b)(a−b)=a2−b2 ・(x+a)(x+b)=x2+(a+b)x+ab数学Ⅰ eテレ 毎週 月曜日 午後2:10~2:30 ※この番組は、21年度の新作です。
先に公式を暗記するより、まずは分配法則をつかって確実に展開できるようになってから公式を覚えたほうが上達も早く、応用にもつよくなる。 (例) (x3)(x5) の展開 (x3)(x5) = x 2 5x 3x 15 = x 2 8x 15 5xと3xは同類項なのでまとめておく。 確認 展開せよ ここでは、組合せの応用として、展開したときの係数を求める問題を考えます。これがわかるようになると、 n 乗の式を展開することなく、係数を求めることができるようになります。 2乗の展開 最終的に $(xy)^n$ を考え 3乗の展開 まとめ お疲れ様でした! 3乗の展開公式は、ちょっと複雑に見えてしまうので苦手な人が多いです。 ですが、やっていることは至ってシンプル! 3乗フォーメーションである 3⇒321⇒312⇒3 これをしっかりと覚えておけば大丈夫ですね (^^) あと




高校数学 数 勉強動画 展開 応用編の問題 19ch




高校数学 マクローリン展開 関数の整式近似 とオイラーの公式 E Ix Cosx Isinx 受験の月
アポロニウスの円の証明と応用 四平方の定理(図形の面積と正射影) 東大数学(図形問題)のポイントと例題 円に内接する三角形の面積の最大値 正四面体の中心角の2通りの求め方 等周問題に関連する高校数学の問題 垂足三角形の意味と5つの性質 教科書 新編 新しい数学3 東京書籍, 単元 多項式の計算,因数分解,式の計算の利用, 「中学校3年生の展開・因数分解を利用した応用問題を解いたノートです。 授業ノートなので見にくいところはあしからず SPというのは先生が作ってくださったオリジナルのスペシャル問題という意味です〇 vi~ixの3次式は高校数学で新たに登場する. 前後の項目 内容が難しいと感じるときは,中学3年の教材を先に読んでください. 前後の項目 展開公式の応用問題は,別のページです.




モデルを志向した数学教育の展開 応用指向vs構造指向 を超えて 敏和 池田 本 通販 Amazon




展開 因数分解 応用編 クイズメーカー こたえてあそぶ つくってあそぶ クイズのプラットフォームサービス
数学16章空間図形「空間図形の展開図・投影図」<応用問題②> 組 番 名前 右の図のように,立方体に「千葉」とかきました。 この立方体を展開図が下の図になったとき,「千」の 字はどの面にあり,向きはどのようになりますか。13 第2 章 Fourier 級数 本章と引き続く幾つかの章で, Fourier 級数とFourier 変換, それらの応用について述べ るFourier とはフランス人Jean Baptiste Joseph Fourier (1768 10) のことで, 彼は 数学者, 技術者として活躍し, Napoleon に仕えた人物である 12 年に熱伝導に関する 書籍(The´orie analytique de la chaleur)を 高校数学で学習する式の展開の単元から 置き換え、組み合わせ、計算順序 を工夫して展開する問題を解説します。 展開の基礎である以下の公式は使いこなせるものとしてお話を進めていき



数と式 整式の展開に関する問題を解いてみよう 日々是鍛錬 ひびこれたんれん




高校数学復習記録 その2 桜花 現役バイト塾講師 Note
中学生のための数学学習支援、練習問題のダウンロード、家庭学習、定期テスト対策、受験勉強にお役立てください 中学・学習サイト ~勉強法と練習問題 英 数 国 理 社 top > 数学練習問題 > 展開(基本問題1) 社会 歴史 練習問題;高校数学の基本問題 Gogle site →数ⅠA →数ⅡB →数Ⅲ (旧C) ***最近の更新*** 反復試行の確率(入試問題) 絶対値付き関数の定積分 Rの関数hist () Rの関数sample () 名義尺度データの比率の検定 フィッシャーの正確Amazonで敏和, 池田のモデルを志向した数学教育の展開 「応用指向vs構造指向」を超えて。アマゾンならポイント還元本が多数。敏和, 池田作品ほか、お急ぎ便対象商品は当日お届けも可能。またモデルを志向した数学教育の展開 「応用指向vs構造指向」を超えてもアマゾン配送商品なら通常配送




高校数学 展開の工夫 共通部分の置き換え 受験の月
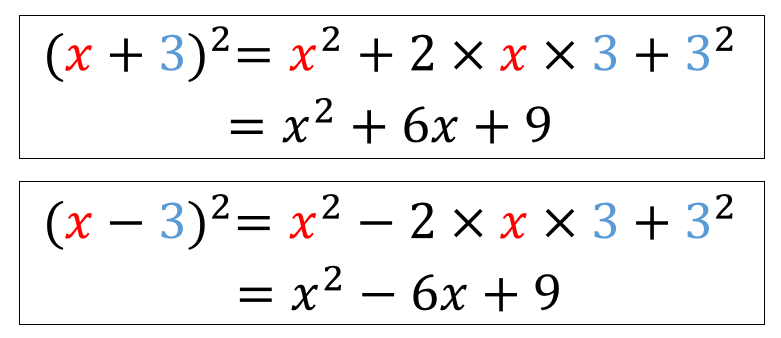



中3数学 展開の公式のやり方は 問題を使って徹底解説 数スタ
70 第9 章応用数学 1 v =2 √ 1 − u v =2 √ 1u v =4 √ 4 − u v =0 4 u v 2 (2) 右図の原像をz 平面上に図示せよ (60 東大) 2 4 e±iθ = cosθ ±isinθ(復号同順) の関係を用いて, 次の問に答えよ ただし, i2 = −1 (1) tanθ = eiθ −e−iθ i(eiθ e−iθ) を証明せよ (2) sinθ = ∞ n=0 a nθ 2n1 と展開するとき, a を求め 中学3年生で学習する展開の計算 中3数学展開の公式のやり方は?問題を使って徹底解説! この展開の計算の中で、もっとも応用なのが次のような計算です。 $$\Large{2(a2)(a3)(a4)^2}$$ うげぇ かっこがたくさんあって複雑じゃ高校講座home >> 数学Ⅰ >> 第4回 数と式 式の展開と因数分解の応用;




中学3年生 数学 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




中3 中3 数学 多項式 中学生 数学のノート Clear
題に応用できるようになる. Contents 1 導入 2 応用例5:漸近展開による不定形の極限計算 3 応用例6:漸近展開による関数の極値判定 4 応用例7:関数のべき級数展開(マクローリン展開) 5 発展事項:オイラーの等式 黒田紘敏(数学部門) 微分積分学I 年6 月動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru応用数学(塩田)年度 前へ / 戻る / 次へ 偶関数・奇関数のフーリエ係数 Rem9 f (x) f ( x) のフーリエ係数について f (x) f ( x) が偶関数ならば bn = 0 b n = 0 ( ∀n ≧ 1 ∀ n ≧ 1 ) f (x) f ( x) が奇関数ならば an = 0 a n = 0 ( ∀n ≧ 0 ∀ n ≧ 0 ) が成り立ちます



1



Fdkyb3b9c093sr81e Com E7 Ba E7 8e 87 E7 B5 B1 E8 A8 2 E9 A0 85 E5 B1 95 E9 96 8b 81 Ae E5 Bf 9c E7 94 A8
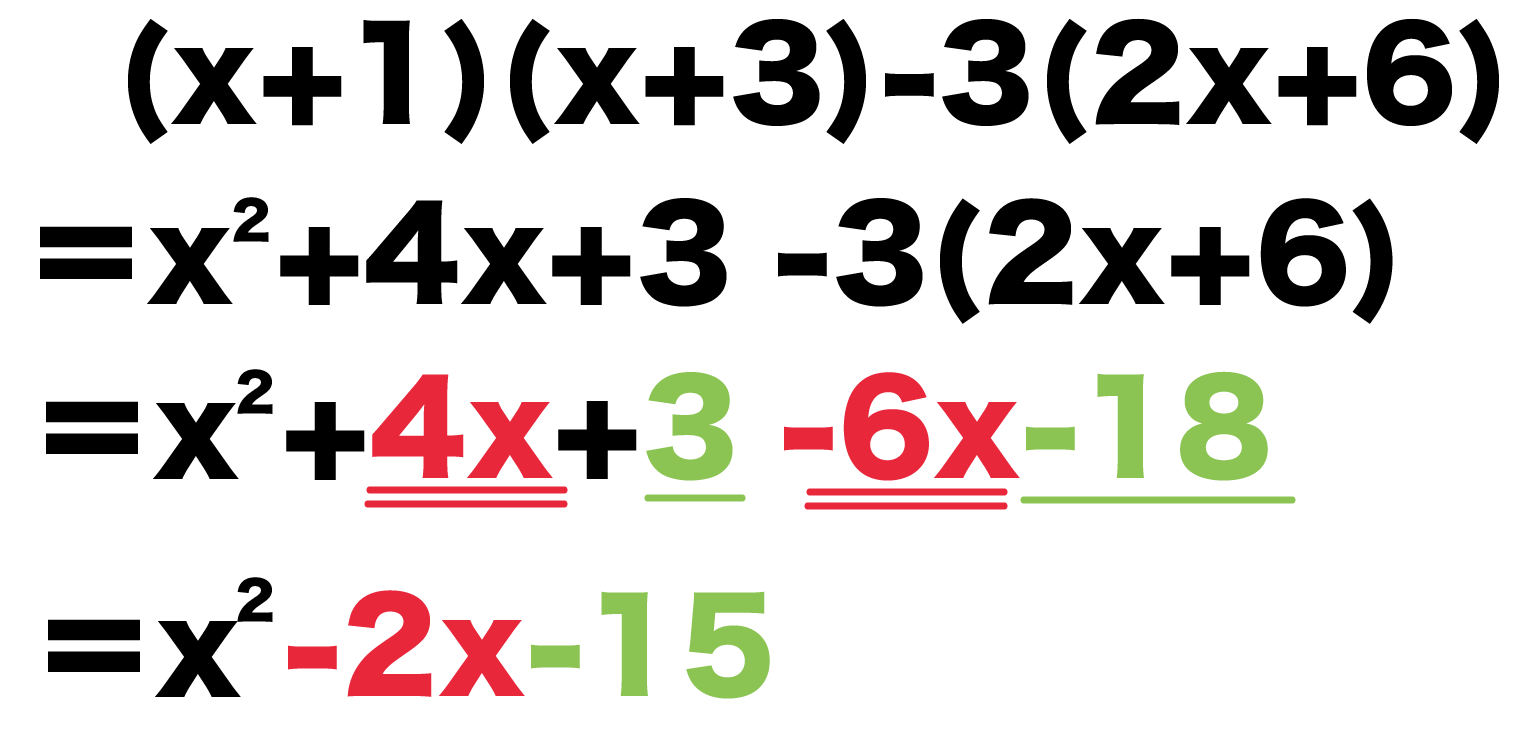



中学数学 式の展開の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




展開 因数分解 練習問題 標準レベル 展開 因数分解の利用 清水塾
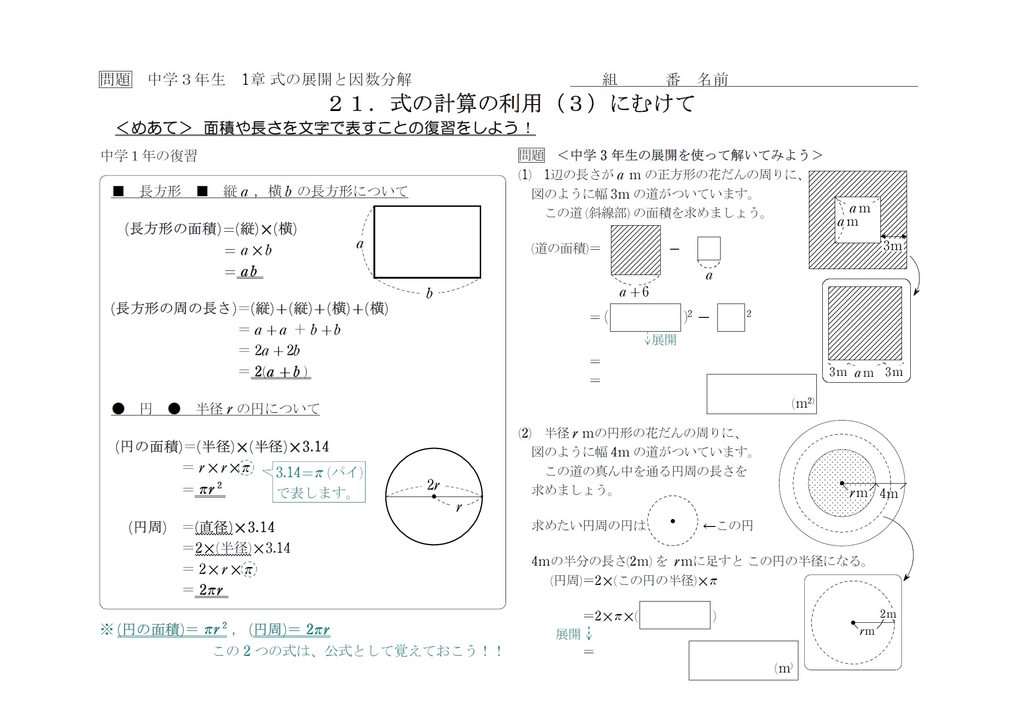



中3自習 展開と因数分解 1 中学数学の勉強に




中3 展開と因数分解8 動画 いろいろな展開 レベル3の解説 中学数学の勉強に




高2数学iiです 二項定理の応用が分かりません 練習11の解き方を教えて下さい Clear




ワークショップ 数学の展開 諸分野との連携を探る 応用数学連携フォーラム Amf




対応分析の理論と実践 基礎 応用 展開 理工学専門書 理学 数学 Ohmsha



中学3年数学練習問題 式の利用 証明 式の展開 因数分解の応用




数学 A B C 二乗の展開公式は 問題の解き方は徹底解説 数スタ




中3数学 乗法公式 応用 置き換え 1 Youtube




式の展開 中3のいろいろな展開問題 乗法公式を使いこなそう 中学数学をはじめから分かりやすく



Q Tbn And9gcseaoibb5sonzvtp 2ugxnyosqkq18ky92debj3yv4tfk5 1rgu Usqp Cau



展開公式



U9j580gf8iba369ji2w Xyz P 614




7題で展開が一気に理解できる 看護学校の受験数学 中学数学 を分かりやすく図解で説明 Kazアカデミー 大阪の看護学校 看護予備校




中3数学 展開とは 練習編 映像授業のtry It トライイット




マクローリン展開の応用例まとめ 高校数学の美しい物語




基礎編 数学の 式の展開 でつまずいたらココを見直そう まなビタミン



中学校3年生式の展開 因数分解分野応用問題 中学3年生の数学の授業で Yahoo 知恵袋




展開の公式応用編3 看護学校の受験数学 中学数学 を分かりやすく図解で説明 Kazアカデミー 大阪の看護学校 看護予備校
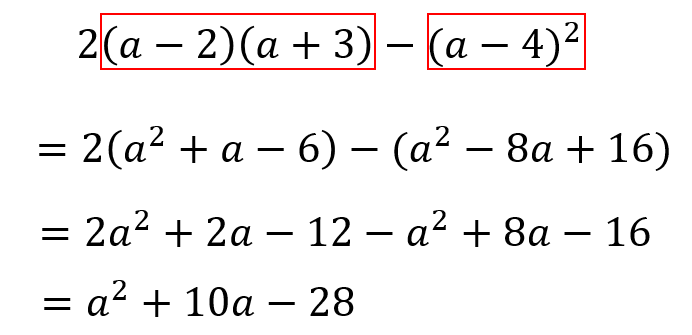



中3数学 複雑な式の展開をマスターしよう 数スタ




中学3年数学 3項式の展開 Youtube



展開公式




中3 式の計算 因数分解 応用編 基本の理解で組立ok 難問と勉強の取組みについて 教えたい 人のための 数学講座




無料 中3数学 発展 応用問題 問題プリント 305 式の計算5 因数分解1




部分分数分解の主要パターン おいしい数学




中学数学 多項式 の教え方 展開の基本




展開 6 ストレートクロスの応用 怜悧玲瓏 高校数学を天空から俯瞰する




高校 数学 因数 分解 難問



Studydoctor A B A B の展開 中3数学 Studydoctor



中3数学 式の展開 応用まで 横井学院予備校のブログ



高校数学1の因数分解の応用編の問題なのですが 下の写真の 2 と 3 の Yahoo 知恵袋




多点総和法入門 高校生でもわかる ココと無限のかなたをつなぐ現代応用数学 テイラー展開から微分方程式の応用まで 上岡 良季 数学 Kindleストア Amazon



公式いろいろ 因数分解のいろいろな問題とその解き方 スタディクラブ情報局



Q Tbn And9gctvyxsiane6xsfgba5 Aeuwoo0bsffzdws04eudn0eg3sgi5vzu Usqp Cau



テーラー展開とマクローリン展開 京極一樹の数学塾




因数分解の応用問題の解き方 現役塾講師のわかりやすい中学数学の解き方




三乗の公式 展開と因数分解 高校生向け受験応援メディア 受験のミカタ




中3数学 カッコ カッコの公式の応用2 練習編 映像授業のtry It トライイット



改訂版 4step数学 P6 1 3次式の展開と因数分解




漸近展開の通販 大久保 謙二郎 河野 実彦 紙の本 Honto本の通販ストア




高校数学 展開公式の利用 受験の月




展開 因数分解を利用した計算の工夫 無料で使える中学学習プリント



岩下の研究への取り組み方 学生向け



数学展開応用公式を用い 工夫して展開せよ A B C 2 Yahoo 知恵袋




Lr07 028 冨永教育経営研究所 ミラクルロード数学 中2 3計算 展開と因数分解 平方根 2次方程式 関数 応用 など 8冊 冨永賢宏 S2d の落札情報詳細 ヤフオク落札価格情報 オークフリー スマートフォン版
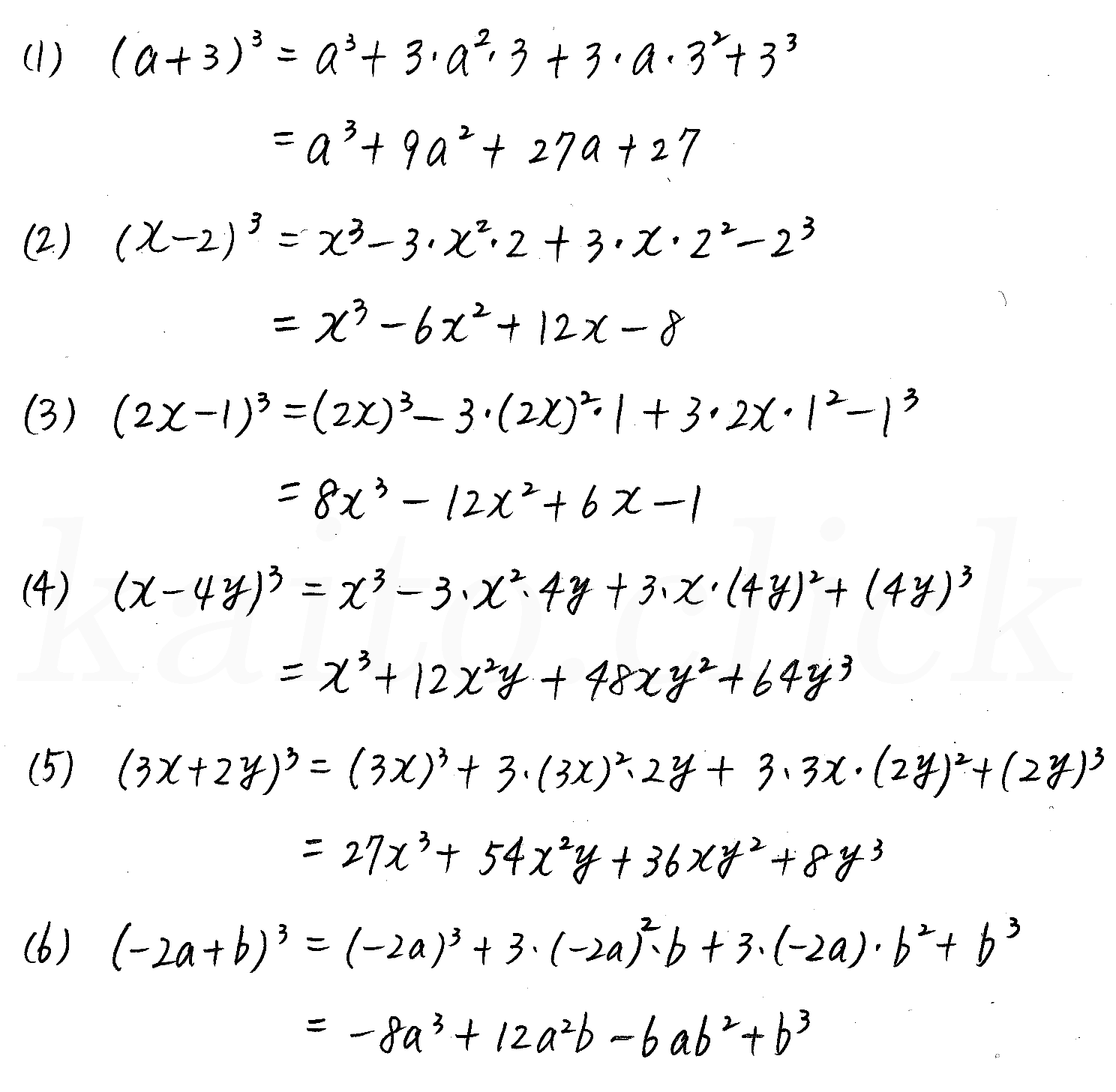



改訂版 3trial数学 P6 1 3次式の展開と因数分解



乗法公式とは 1分でわかる意味 公式の覚え方 問題 因数分解との関係




数と式 整式の展開と乗法公式について 日々是鍛錬 ひびこれたんれん




中3数学 複雑な式の展開をマスターしよう 数スタ



Studydoctor3項式の展開 中3数学 Studydoctor




高校数学 数 7 展開 3次式の公式編 Youtube



2




式の展開 中3のいろいろな展開問題 乗法公式を使いこなそう 中学数学をはじめから分かりやすく




中学3年数学 3項式の展開 Youtube




中学3年数学練習問題 式の利用 証明 式の展開 因数分解の応用




展開因数分解の式の値の応用 対称式と交代式 中3数学 高校受験ラボ




中学3年生 数学 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




高校数学 数 10 因数分解 応用編 Youtube




乗法公式 無料で使える中学学習プリント



中1数学 発展 応用問題プリント 空間図形の位置関係 140




アルアカ در توییتر 先日 生徒から質問があった問題とその応用の仕方です 因数分解で 押してダメなら引いてみろ です 確かに高一ならあまり直接役立ちませんが 今後応用できます まあ 三つの項の二乗の展開は流石に知っているものとしています 数学




7題で展開が一気に理解できる 看護学校の受験数学 中学数学 を分かりやすく図解で説明 Kazアカデミー 大阪の看護学校 看護予備校




三乗の公式 展開と因数分解 高校生向け受験応援メディア 受験のミカタ
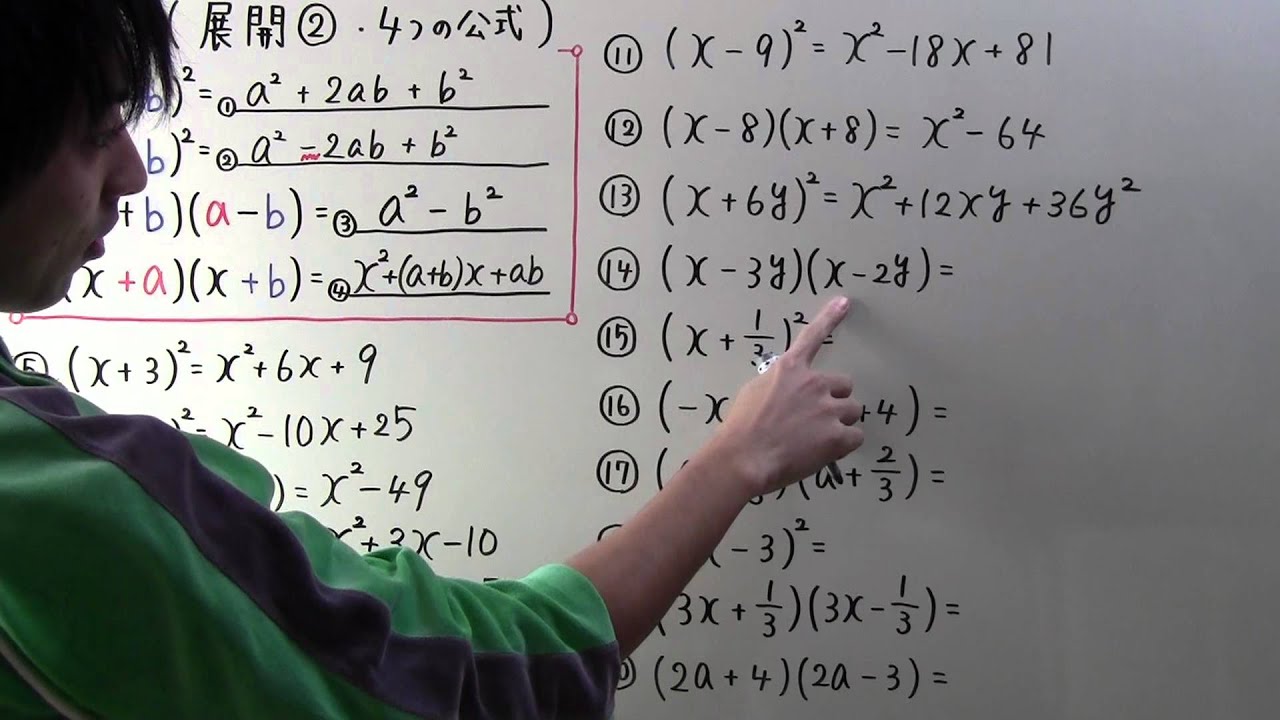



数学 中3 3 展開 4つの公式 Youtube




数学 中3 9 因数分解 もっと応用編 Youtube




中3数学 式の展開 因数分解がスラスラ解ける 魔法の授業 学校 塾 家庭教師の1カ月分が1本の動画に On Vimeo




中学数学 多項式 の教え方 展開の応用問題



中1数学 発展 応用問題プリント 空間図形の展開図と多面体 139



数と式の問題 Of 京極一樹の数学塾会員頁




高校数学復習記録 その2 桜花 現役バイト塾講師 Note




ベンゾオキサジン樹脂の新しい設計と応用展開 シーエムシー出版 物理 化学 数学 通販モノタロウ




中3 展開 因数分解の応用 トリセツ終わった人へ Nikkeyweb Rede Da Comunidade E Da Cultura Japonesa No Brasil



数と式の問題 京極一樹の数学塾




高校数学 二項定理 A B Nの展開式 整式の係数の和 受験の月




高校数学 多項定理 A B C Nの展開式の係数 受験の月



数と式の問題 Of 京極一樹の数学塾会員頁




高校数学 展開のおさらい1 映像授業のtry It トライイット




書記が数学やるだけ 103 テイラー展開とその応用 誤差評価 漸近展開 鈴華書記 Note




マリアバン解析と漸近展開の応用 日本数学会




高認 数学1 第1章 式の計算 展開応用 Youtube



1




ルート計算 展開公式をつかう3つの平方根問題の解き方 Qikeru 学びを楽しくわかりやすく
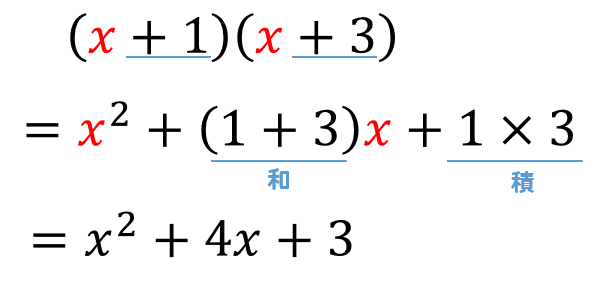



中3数学 展開の公式のやり方は 問題を使って徹底解説 数スタ




漸近展開 1976年 シリーズ新しい応用の数学 12 一松信 伊理正夫 竹内啓編 本 通販 Amazon




展開公式1 数学の基礎とその計算を理解しよう Rikeinvest




高校数学 数 第1章 数と式 3 展開公式 2項の3乗の展開公式 壱のblog




高校数学 数 6 展開 応用編 Youtube




展開の公式応用編1 看護学校の受験数学 中学数学 を分かりやすく図解で説明 Kazアカデミー 大阪の看護学校 看護予備校




モデルを志向した数学教育の展開 応用指向vs構造指向 を超えて 敏和 池田 本 通販 Amazon
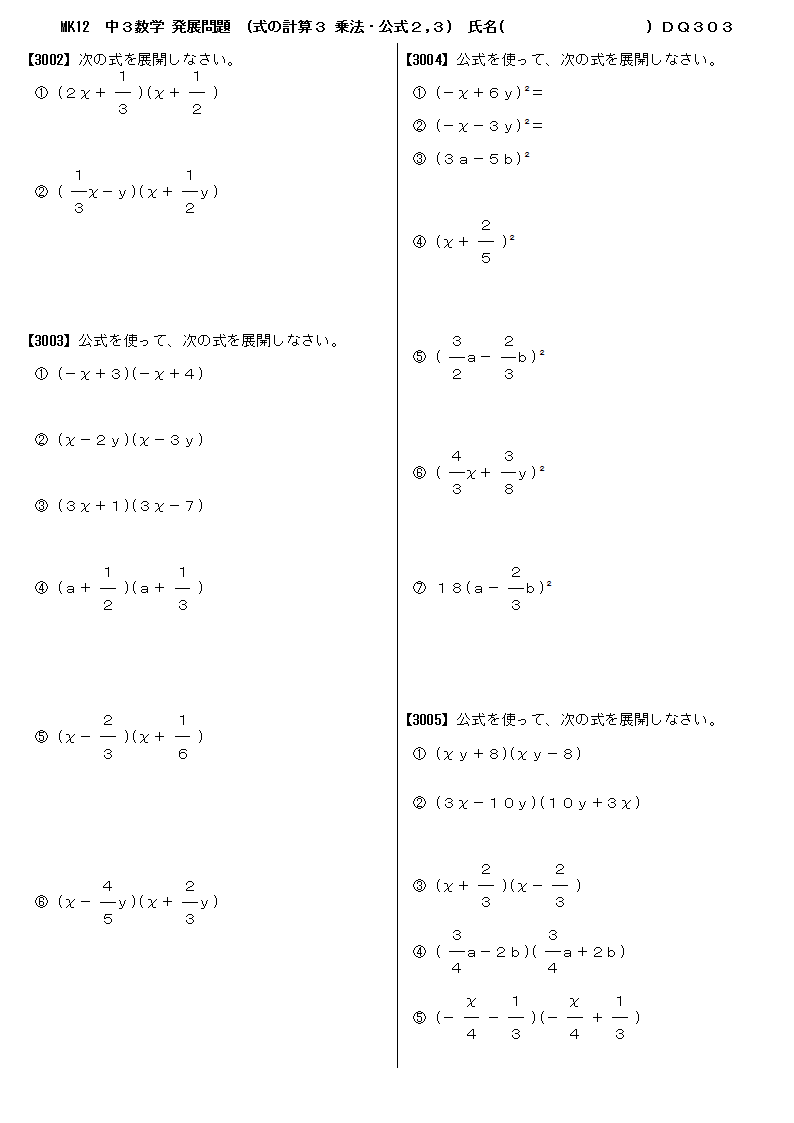



無料 中3数学 発展 応用問題 問題プリント 303 式の計算3 乗法 公式2 3




中学数学 多項式 の教え方 展開の応用問題



0 件のコメント:
コメントを投稿